
今回はコンピュータで必要となる基礎知識である計算関係の話をするよ。
コンピュータ関係ではあるけどどちらかというと数学に近いからかなり馴染み深いと思う。

数学…受験を思い出すなぁ

ぼ、ぼくは一応理系なので数学ならいけそうな気がします!

コンピュータは0と1の世界というのはどこかで聞いたことあると思う。
0と1っていうのは電気信号で言うところのオフとオンかを表しているんだけど、今回はそんな話で出てくる0と1の世界・2進数について説明していくよ。
2進数
コンピュータは電気信号で動いているのは知っていると思う。
そんな電気信号にはオンの状態とオフの状態がある。その状態をうまく利用することでコンピュータは複雑な処理というのができているんだ。
オンとオフ、二つの状態を0と1で表すからコンピュータの世界は0と1という2進数で表現されるんだよ。
2進数とは

そもそも2進数ってなんですか?
2進数というのは0と1しか数字を使わない数を表す方法を言うよ。

コンピュータが0と1で処理が進むイメージがあんまりつかないんですが…
電球をイメージするとわかりやすいと思う。例えば、電球Aがあるとする。
この時Aが点灯すれば晴れ、Aが消えている場合は雨と言うのが表現できるようになるんだ。
仮にこれが二つの電球AとBになった時は、点灯と非点灯の組み合わせが4つ生まれて4つの表現が電球のオンオフによって表せることになるよ。

点灯のオンオフ、つまりは1か0かってことで表現できてしまうってことですね。

なるほど~、私たちが普段目にしているのはじゃあ何なんですか?
0と1だけじゃなく2も3も9もありますよね
僕たちが普段目にしているのは10進数と呼ばれるものだよ0~9までの数字で表現される方法で、ちなみに時計は12進数。
ITの世界では2進数と10進数を変換し合うことで、日常の計算をコンピュータにさせたり、コンピュータの計算を日常的な計算結果として僕たちが受け取れるようにするんだ。
2進数 ⇄ 10進数
2進数と10進数は双方向に変換ができるんだ。
例えば、10進数で12を表す場合、2進数では1100となるよ。
2進数をわかりやすい形でするとこんな感じの図になる。
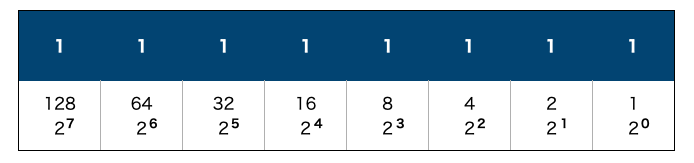
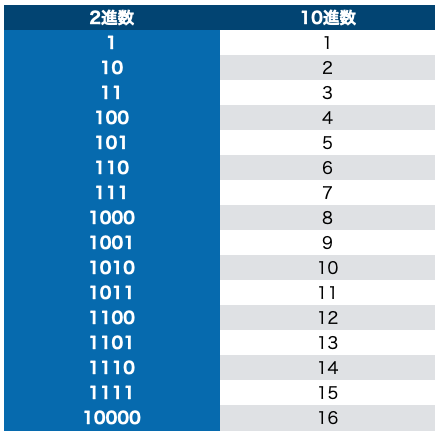
ちなみに10進数との対応表を作るとこんな感じになる。
一番下のくらいは○進数の○^0を表していて、次の位は○^1、次は○^2…となっていく。

ちょっとすいません、^2ってなんですか?見たことない記号なんですけど。
^はべき乗を表しているよ。
^2ならば2乗(2×2)を表している。
コンピュータではなんちゃら乗って言う表現が難しいからわかりやすい記号を使って^で表現するんだ。

もしかして、10進数を2進数にする場合はいちいちこの図を思い出して、組み合わせを一つずつ試していくんですか?
それでももちろん回答に辿り着くことはできるけど、面倒すぎるから計算のコツがあるんだ。
ズバリコツは「2進数で割った答えを2で割って行って最後に余りを辿る方法」だ。
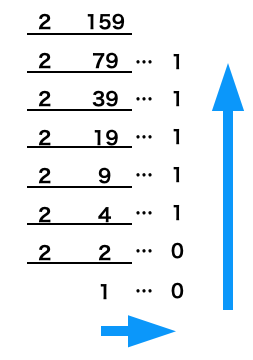
159を例題として2進数に直していくよ。
159÷2の答えは、79あまり1
159÷2の答え79、に対して割る2をして、39あまり1
39÷2をして、19あまり1
19÷2をして、9あまり1
9÷2をして、4あまり1
4÷2をして、2あまり0
2÷2をして、1あまり0
割った答えが1になったら計算終わり。
最終的な答え1と余りを辿っていって「10011111」となる。つまり159を2進数で表した答えは「10011111」となるんだ。
ちなみに、解き方を図で表すとこんな感じ、こんな感じで筆算に似た図を書きながら解くとどんな難しい10進数も2進数に直すことができるんだ。
2進数から10進数に直す場合は、地道に位ごとの2のべき乗を計算して足していくしかない。
101という2進数を10進数に直す場合は、1の位は2^0だから1、二つ目の位は2^1で2×0だから0、三つ目の位は2^2で4×1だから4、合計して101の10進数は5とわかるんだ。

10進数から2進数はすごい簡単そうですけど、2進数からだと面倒臭いですね。

そうだね。
問題の傾向としても基本的に10進数→2進数というのが多いから、仕組みだけ抑えておけば大丈夫だと思うよ!
2進数の足し算
2進数の足し算も出題されることが多いよ。
手順は10進数と基本的には一緒で注意点としては1の次は2ではなく、位が上がるという点だけ。
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10(桁が上がる)
この4つの仕組みさえ押さえておけば解けるんだ。
例題として1010 + 1111を計算してみよう。
筆算の図を見てみて。
注意点としては「1 + 1」があるところ、桁が上がることに注意して。

なるほどですね。
じゅ、10進数では10になる時点で桁が上がるのが2進数だと2で桁が上がる仕組みがわかってしまうと単純なんですね。

そう、10進数の計算も2進数の計算もあとは問題を解いていくうちに慣れてくるから問題をどんどんやっていくのが一番だね!
集合と論理演算
続いてコンピュータで使われることが多い集合という概念と論理演算、確率について説明していくよ。
ベン図とは
そもそもベン図というのは、グループ(集合)同士の関係を視覚的に表現するものだよ。
集合の関係には下の4つの種類がある。
AND(かつ):論理積
OR(または):論理和
NOT(ではない):否定
XOR(片方だけ):排他的論理和
この四つの集合関係を図で表したのがベン図なんだ。
具体例を上げながら4つの状態を表現するとこんな感じかな。
論理積:「パソコンを持っている」かつ「iPhoneを持っている」ヒト。どっちも持っているヒト。
論理和:「パソコンを持っている」または「iPhoneを持っている」ヒト。どっちかを持っているヒトだね。
否定は論理積、や論理和、排他的論理和と組み合わせて使うもので、論理積と組み合わせると「パソコンを持っていないかつiPhoneも持っていないヒト」というのが表現できたりするんだ。
排他的論理和:「パソコンを持っている」か「iPhoneを持っている」かどっちかだけのヒト。どっちかしか持っていない場合のヒトだね。

あ!これ昔数学でやった気がします!
全然内容覚えてなかったですけど、これってコンピュータとか関わっているんですね。
集合とコンピュータの関係
集合・ベン図がわかったところでコンピュータの関係についても紹介しておく。
コンピュータは0と1で表現されるっていったけど、その際にある値が1か0かつもう一つの値が1か0の場合は何かをするっていう表現をするために集合やらベン図が使われるんだ。

ご、ごめんなさい、いまいち実感が湧かないです…
例えば、晴れているかつ地面が乾いている時にだけ花に水をやる処理をしたいと考えよう。
この時晴れているという条件が1を表した時、かつ、地面が乾いているという条件を表す1という値が二つ揃った時初めて花に水をやるという処理をすることになる。
晴れていない場合は0、乾いておらず湿っている場合は0として考えると真理値表としてこうやって書くことができるようになる。

あ!な、なるほど
ここで全部が1のときに水やりという処理が動き出すようにプログラムをするとかって話ですか?

まさにその通り、条件を組み合わせるときに集合やらベン図が重要になってくるんだ。
なんの条件が1のとき処理が動き出すとかを考える時とかに情報を整理するために利用されたりするんだ。
確率
試験には確率も出てくるから、中学校高校の復習も兼ねて押さえておこう。
確率とは
確率とは、ある事柄が起こりうる可能性の度合いのこと。
例えば52枚のトランプのうちスペードを引く確率を考える。
この時トランプのスペードのマークがあるのは13枚だから、52枚のうち13枚のいずれかを引けば良いということになるから。
確率は13/52=1/4となる。
公平に起こりうる場合を前提にしているけど、こうすることで何か事柄が起きる前に可能性を考えることができるのが確率だったね。

これは割と覚えてましたね!降水確率とかも天気予報で聞くので結構身近な気がします。
確率の足し算、かけ算
確率は一個だけじゃなく何度も行われる時足し算や掛け算が必要になってくるんだ。
例えば、サイコロの目が連続して出る場合は掛け算を使う。逆に同時に起こる場合は足し算をして計算を考える。
サイコロの目が1が2回連続で発生する確率は、1/6×1/6=1/36となる。
サイコロの目が1または2が出る確率は、1/6+1/6=2/6=1/3となるんだ。
これは同時に発生しうるかどうかによって見極めて使い分けるよ。

完全に数学の話ですね。受験とかを思い出します。

私ちょっと忘れてたところあるから高校の教科書でも引っ張ってきますね笑
期待値
最後に期待値を解説するね。
期待値とは、見込みのことを表すよ。宝くじを300円買って1億円を手にいれる場合、300円で期待値が1億円となる。
期待値は計算式で、下記のような当たる確率を算出した後で戻ってくる利益を使って算出することができるんだ。
三つの広告を打つ場合それぞれの費用対効果と確率は下記表
ダイレクトメール:費用3、50%で5の利益、40%で4の利益、10%で2の利益
CM:費用15、50%で20の利益、40%で25の利益、10%で12の利益
インフルエンサー起用:費用6、50%で10の利益、40%で15の利益、10%で8の利益
それぞれの期待値は、下記となる。
ダイレクトメール:0.5×5 + 0.4×4 + 0.1×2 = 4.3
CM:0.5×20 + 0.4×25 + 0.1×12 = 21.2
インフルエンサー起用:0.5×10 + 0.4×15 + 0.1×8 = 11.8
ここに費用をでそれぞれ引いてあげると、
ダイレクトメール:4.3 – 10 = 1.3
CM:21.2 – 15 = 6.2
インフルエンサー起用:11.8 – 6 = 5.8
つまり、CMを使うのが一番期待値も費用対効果も大きいというのがわかるんだ。
まとめ

どうだった?かなり数学的な話だったけど、ついてこれたかな?

はい、懐かしい思い出できましたね。

私はちょっと思い出せないことありましたけど、なんとか計算を理解することはできました。

コンピュータの基礎的な部分はこういった2進数やベン図・集合の話だからここは基礎としてしっかり押さえておこうね。
問題を解いていくとさらにコツを掴めると思うから、この先はぜひ問題集を買って、解いてみることをおすすめするよ。

資格試験は問題を解くほど理解が深まって合格に近づくからね。
おすすめの問題集はこれだから買っておくと合格に近づけるよ。
じゃあ今回はこの辺で、また次回!

はい!ありがとうございました!!
 てっぱんITクラブ
てっぱんITクラブ


